plus one maths previous year question papers and answers pdf download

All plus one maths previous year question papers and answers pdf download:
| Board name | SCERT, Kerala Board |
| Textbook type | NCERT Based |
| Class | Plus One |
| Subject | Maths |
| Papers | Previous Papers, Model Papers, Sample Papers |
| Category | Kerala Plus One |
Plus One Maths Previous Year Question Papers and Answers Kerala direct links:
HSE Kerala Board Syllabus Plus One Maths Previous Year Model Question Papers and Answers Pdf Free Download in both English medium and Malayalam medium are part of SCERT Kerala Plus One Previous Question Papers and Answers. Here we have given Higher Secondary Kerala Plus One Maths Previous Year Sample Question Papers with Answers based on CBSE NCERT syllabus.
| Board | SCERT, Kerala Board |
| Textbook | NCERT Based |
| Class | Plus One |
| Subject | Maths |
| Papers | Previous Papers, Model Papers, Sample Papers |
| Category | Kerala Plus One |
Here Plus One Maths Previous Year Question Papers and Answers list:
- Plus One Maths Previous Year Question Paper March 2019
- Plus One Maths Previous Year Question Paper March 2018
- Plus One Maths Previous Year Question Paper March 2017
- Plus One Maths Improvement Question Paper Say 2018
- Plus One Maths Model Question Papers Paper 1
- Plus One Maths Model Question Papers Paper 2
- Plus One Maths Model Question Papers Paper 3
- Plus One Maths Model Question Papers Paper 4
Kerala Plus One Maths Previous Year Question Paper March 2019 with Answers
| Board | SCERT |
| Class | Plus One |
| Subject | Maths |
| Category | Plus One Previous Year Question Papers |
Time Allowed: 2 1/2 hours
Cool off time: 15 Minutes
Maximum Marks: 80
General Instructions to Candidates :
- There is a ‘cool off time’ of 15 minutes in addition to the writing time.
- Use the ‘cool off time’ to get familiar with the questions and to plan your answers.
- Read instructions carefully.
- Read questions carefully before you answering.
- Calculations, figures and graphs should be shown in the answer sheet itself.
- Malayalam version of the questions is also provided.
- Give equations wherever necessary.
- Electronic devices except non programmable calculators are not allowed in the Examination Hall.
Answer any 6 from questions 1 to 7. Each question carries 3 score. (1 × 6 = 6)
Question 1.
Let A = {x: x is a prime number less than 11} and B = {x: x is an integer such that 2 ≤ x ≤ 8}.
(i) Write C = A ∩ B.
(ii) Find the number of subsets of C which has 3 elements.
(iiii) What is the probability of getting a subset of 3 elements from the power set of C.
Answer:
(i) A = {2, 3, 5, 7}; B = {2, 3, 4, 5, 7, 8}
C = {2, 3, 5, 7} ∩ {2, 3, 4, 5, 7, 8} = {2, 3, 5, 7}
(ii) Number of subsets of C which has 3 elements
= 4C3 = 4
(iii) Probability of getting a subset of 3 elements from the power set of C
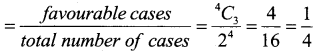
Question 2.
(i) Find(a + b)4 -(a – b)4.
(ii) Hence evaluate
(3‾√ + 2‾√)4 – (3‾√ – 2‾√)4.
Answer:
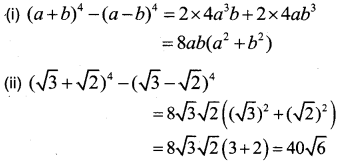
Question 3.
Find the square root of the complex number 3 + 4i.
Answer:
Let x + iy = 3+4𝑖‾‾‾‾‾‾√
Then (x + iy)2 = 3 + 4i
⇒ x2 – y2 + 2xyi = 3 + 4i
Equating real and imaginary parts, we have
x2 – y2 = 3 ……… (1)
2xy = 4
We know the identity
(x2 + y2)2 = (x2 – y2)2 + (2xy)2
= 9 + 16 = 5
Thus, x2 +y2 = 5 …….. (2)
From (1) and (2), x2 = 4 and y2 = 1 or x = ±2 and y = ±1
Since the product xy is positive,
we have x = 2, y = 1 or, x = – 2, y = -1
Thus, the square roots of 3 + 4i are
2 + i and -2 – i.
Question 4.
The sum of first three terms of a Geometric Progression is 1312 and their product is -1. Find the common ratio and the terms.
Answer:
Let 𝑎𝑟, a, ar be the numbers.

Question 5.
Find the solution of the equation
sinx + sin3x + sin5x = 0
Answer:
sinx + sin3x + sin5x = 0
2 sin3x cos2x + sin3x = 0
⇒ sin3x (2 cos2x + 1) = 0
⇒ sin 3x = 0; 2 cos 2x + 1 = 0
⇒ 3x = nπ, n ∈ Z; 2 cos2x = -1
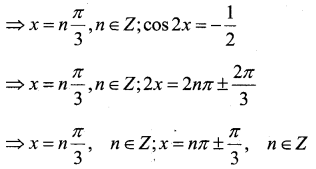
Question 6.
Consider the graph of the function f(x)
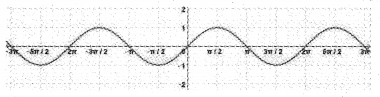
(i) Identify the function f (x)
(a) f(x) = sinx (b) f(x) = cos x
(c) f(x) = tanx (d) f(x) = cos ecx
(ii) Using the function f(x) find
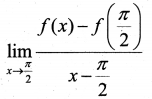
(i) (a) f(x) = sinx

Question 7.
(i) Find the general term in the expansion of (𝑥2+1𝑥)5.
(ii) If the expansion of (𝑥2+1𝑥)𝑛 has a term independent of x, then which of the following can be the value of n?
(a) 18 (b) 16 (c) 22 (d) 13
Answer:
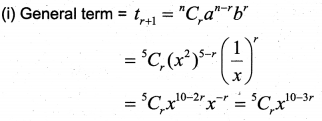
(ii) For getting a term independent of x in the expression of (𝑥2+1𝑥)𝑛, power of x
2n – 3r = 0 ⇒ n = 3𝑟2
Which means n should be a multiple 3 and divisible by 2. Hence (a) 18.
Answer any 8 from questions 8 to 17. Each question carries 4 scores. (8 × 4 = 32)
Question 8.
In a school, a survey among 400students, 100 were listed as taking apple juice, 150 as taking orange juice and 75 were listed as taking both apple juice as well as orange juice.
(i) How many students take apple juice or orange juice?
(ii) How many take apple juice alone but not orange juice?
(iii) How many students were taking neither apple juice nor orange juice?
Answer:
Let A: Apple juice, O: Orange juice.
(i) n(A ∪ O) = n(A) + n(O) – n(A ∩ O)
= 100 + 150 – 75 = 175
(ii) n(A ∩ O’) = n(A) – n(A ∩ O)
= 100 – 75 = 25
(iii) n(A’ ∩ O’) = 400 – n(A ∪ O)
= 400 – 175 = 225
Question 9.
The figure shows the graph of the function f(x).
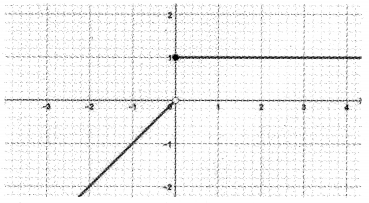
(i) Write the domain and range of f(x).
(ii) Find f(0)and f(-0.01).
(iii) Check the existence of lim𝑥→0 f(x).
Answer:
(i) Domain = R
Range = (-∞, 0) ∪ {1}
(ii) f(0) = 1, f(-0.01) = -0.01
(iii) lim𝑥→0− f(x) = 0, lim𝑥→0+ f(x) = 1
lim𝑥→0− f(x) = lim𝑥→0+ f(x)
Therefore limit does not exists.
OR
There is a break in the graph of f(x) at x = 0.
So limit does not exist at x = 0.
Question 10.
Consider the set A = {-1, 1}
(i) Write all elements is A × A.
(ii) How many relations are there from A to A?
(iii) Write all functions from A to A which has Range = {-1, 1}.
Answer:
(i) A × A = {(-1, -1), (-1, 1), (1, -1), (1, 1)}
(ii) Number of relations = 2n(A × A) = 24 =16
(iii) There are two functions
f1 ={(-1, -1), (1, 1)}
f2 = {(-1, 1), (1, -1)}
Question 11.
Using principle of mathematical induction prove that n(n +1)(n + 5) is a multiple of 3 for all n ∈ N.
Answer:
p(1) : 1(1 + 1)(1 + 5) = 12 divisible by 3, hence true. Assuming that true for p(k)
p(k) : k(k + 1 )(k + 5) is divisible by 3.
k(k + 1)(k + 5) = 3M
p(k + 1) : (k + 1)(k + 2)(k + 6)
= (k + 1)(k2 + 8k + 12)
= (k + 1)(k2 + 5k + 3k + 12)
= (k + 1) [k(k + 5) + 3(k + 6)]
= [k(k + 1)(k + 5) + 3(k +1)(k + 6)]
= [3M + 3(k + 1)(k + 6)]
= 3[M + (k + 1)(k + 6)]
Hence divisible by 3. Therefore by using the principle of mathematical induction true for all n ∈ N.
Question 12.
If z is a complex number with |z| = 2 and arg(z) = 4𝜋3, then
(i) express z in a + ib form.
(ii) Find 𝑧¯
(iii) Verify that (𝑧¯)2 = 2z
Answer:
(i) z = r(cosθ + i sinθ)
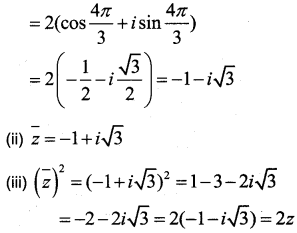
Question 13.
Seven cards are drawn from a pack of well shuffled 52 playing cards.
(i) How many ways this can be done?
(ii) What is the probability that the selection contain all kings?
(iii) What is the probability that selection does not contain a king card?
Answer:

Question 14.
(i) Write the contrapositive of the given statement.
“If a number is divisible by 9, then it is divisible by 3.”
(ii) Verify by the method of contradiction:
“p : 7‾√ is irrational.”
Answer:
(i) If a number is not divisible by 3, it is not divisible by 9.
(ii) Assume that 7‾√ is rational. Then 7‾√ can be written in the form 7‾√ = 𝑝𝑞, where p and q are integers without common factors.
Squaring; 7 = 𝑝2𝑞2 ⇒ 7q2 = p2
⇒ 7 divides p2 ⇒ 7 divides p
Therefore, p = 7k for some integer k.
=> p2 = 49k2 ⇒ 7q2 = 49k2 ⇒ q2 = 7k2
⇒ 7 divides q2 ⇒ 7 divides q
Hence p and q have common factor 7, which contradicts our assumption. Therefore, 7‾√ is irrational.
Question 15.
Calculate the mean deviation about median for the following data:
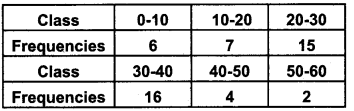
Answer:
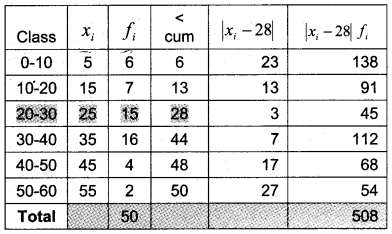
Median class is the class in which the (502=25)𝑡ℎ
observation lies. Therefore median class is 20 – 30.

Question 16.
Consider the word ASSASSINATION
(i) How many different ways can the letters of the word are arranged
(ii) How many of these words have all vowels together?
Answer:
(i) In the word ASSASSINATION there are 13 letters, of which A appears 3 times, S appears 4 times, N appears 2 times, I appears 2 times and the rest all are different.
Therefore the total number of ways is

Question 17.
Let A (0, 7, 10), B(-1, 6, 6,) and C (-4, 9, 6) are the vertices of a triangle.
(i) Show that is a right triangle.
(ii) Find the coordinate of the centre of the circle passing through the point A, B, C.
Answer:
(i) AB2 = (-1 – 0)2 + (6 – 7)2 + (6 – 10)2
= 1 + 1 + 16 = 18
BC2 = (-4 – (-1))2 + (9 – 6)2 + (6 – 6)2
= 9 + 9 + 0 = 18
AC2 =(-4 – 0)2 + (9 – 7)2 + (6 – 10)2
= 16 + 4 + 16 = 36
AB2 + BC2 = AC2
Therefore triangle ABC is right triangle.
(ii) Since the triangle is a right triangle, the circumcentre will lie on the midpoint of the side AC.

Answer any 5 from questions 18 to 24. Each question carries 6 score. (5 × 6 = 30)
Question 18.
The figure shows a unit circle and a line L which makes 30° with the positive direction of x – axis.

(i) Write the equation of the line L.
(ii) Write the coordinate of the points A and B.
(iii) Find the equation of the tangent line to the circle at A.
Answer:
i) The slope of the line L


Question 19.
Consider two lines L1: 2x + y = 4 and L2: (2x – y = 2)
(i) Find the angle between L1 and L2.
(ii) Find the equation of the line passing through the intersection of L1 and L2
which makes an angle 45° with the positive direction of x – axis.
(iii) Find the x and y Intercepts of the third line obtained in part (ii).
Answer:
(i) The slope of the line L1 is -2.
The slope of the line L2 is 2.
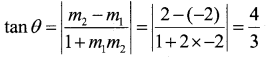
(ii) The family of lines is of the form
L1 + λL2 = 0
⇒ (2x + y – 4) + λ(2x – y – 2) = 0
⇒ (2 + 2λ)x + (1 – λ)y – 4 – 2λ = 0
⇒ Slope = −2+2𝜆1−𝜆 = tan 45 = 1
⇒ -2 – 2λ = 1 – λ ⇒ λ = — 3
Equation of the line is 2x – 2y = 1

Question 20.
If an ellipse passing through (3, 1) having foci (±4, 0), then
(i) find the length of the major axis
(ii) find the standard equation of the ellipse.
(iii) find the eccentricity and length of the latus rectum.
Answer:
(i) Length of the major axis = Sum of the distances of the point (3, 1) from the foci (±4, 0)

Question 21.
(i) Find sin 75°
(ii) The figure shows ΔABC with side AC = 42‾√ units inscribed in a circle of radius 4 units. The length of the arc BDC is 10𝜋3 units.

(a) Write ∠A in degree measure.
(b) Find the length of the sides AB and BC.
Answer:
(i) sin(75°) = sin(45° + 30°)
= sin45° cos30° + cos45° sin30°


Question 22.
(i) Solve 3(𝑥−2)5≤5(2−𝑥)3
(ii) Solve the inequalities
2x + 3y ≤ 12; x ≥ 1; y ≥ 2 graphically.
Answer:
(i) 3(𝑥−2)5≤5(2−𝑥)3
⇒ 9(x — 2) ≤ 25(2 – x)
⇒ 9x -18 ≤ 50 – 25x
⇒ 34x ≤ 68 ⇒ x ≤ 2
(ii)

Question 23.
(i) Find the derivative of y = x2 using the first principle.
(ii) Find 𝑑𝑦𝑑𝑥 if y = 𝑥1+tan𝑥
Answer:

Question 24.
Consider the sequence 3, 6, 9, 12, ….., 99
(i) How many terms are there in the given sequence?
(ii) Find the mean of the sequence.
(iii) Find the sum of squares of each terms of the given sequence.
(iv) Find the variance of the sequence.
Answer:
(i) 3 × 1, 3 × 2, 3 × 3,…….. 3 × 33
Hence there are 33 terms in the given sequence.
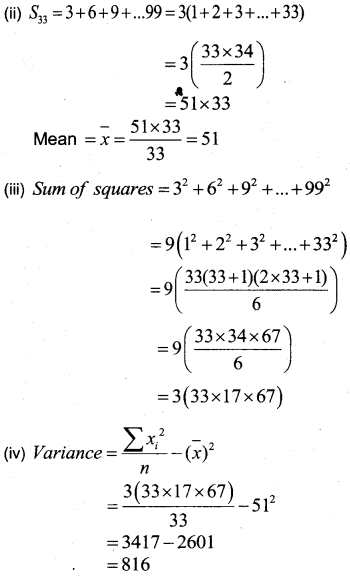
Kerala Plus One Maths Previous Year Question Paper March 2018 with Answers
| Board | SCERT |
| Class | Plus One |
| Subject | Maths |
| Category | Plus One Previous Year Question Papers |
Time Allowed: 2 1/2 hours
Cool off time: 15 Minutes
Maximum Marks: 80
General Instructions to Candidates :
- There is a ‘cool off time’ of 15 minutes in addition to the writing time.
- Use the ‘cool off time’ to get familiar with the questions and to plan your answers.
- Read instructions carefully.
- Read questions carefully before you answering.
- Calculations, figures and graphs should be shown in the answer sheet itself.
- Malayalam version of the questions is also provided.
- Give equations wherever necessary.
- Electronic devices except non-programmable calculators are not allowed in the Examination Hall.
Answer any six questions from 1 to 7. Each carries 3 scores. (6 × 1 = 6)
Question 1.
Find the sum to n terms of the sequence 4 + 44 + 444 + ………
Answer:
Sn = 4 + 44 + 444 +
= 4(1 + 11 + 111 + ………)
= 49(9 + 99 + 999 + ………)
= 49(10 – 1 + 100 – 1 + 1000 – 1 + ……….. )
= 49(10 + 100 + 1000 + …. – 1 – 1 – 1 – ……)
= 49(10 + 102 +103 + …….. -n)
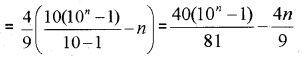
Question 2.
Solve: sin 2x – sin 4x + sin 6x = 0
Answer:
sin 2x + sin 6x – sin 4x = 0
⇒ 2 sin4x cos2x – sin4x = 0
⇒ sin 4x(2 cos2x -1) = 0
⇒ sin4x = 0 or (2 cos2x – 1) = 0
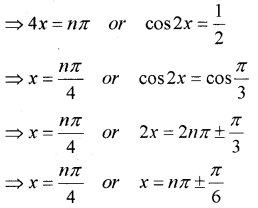
Question 3.
If A and B are events such that
P(A) = 14, P(B) = 12; P(A∩B) = 16
Then find
a) P(A or B)
b) P(not A and not B)
a) P(A or B)= P(A∪B)
= P(A) + P(B) – P(A∩B)
= 14+12−16=3+6−212=712
b) P(not A and not B) = P(A’∩B’)
= P((A∪B)’)
= 1 – P(A∪B) = 1 – 712=512
Question 4.
In a ΔABC , prove that tan(𝐵−𝐶2)=𝑏−𝑐𝑏+𝑐cot𝐴2
Answer:

Question 5.
a) The maximum value of the function f(x) = sinx is ………..
(i) 1 (ii) 3√2 (iii) 12 (iv) 2
b) Prove that; (sin x + cos x)2 = 1 + sin 2x
c) Find the maximum value of sinx + cosx
Answer:
a) a) 1
b) (sinx + cosx)2 = sin2x + cos2x + 2sinx cosx
= 1 + sin 2x
c) The maximum value of sinx is 1, therefore the maximum value of sin2x is also 1.
(sin x + cos x)2 = 1 + sin 2x
sin x + cos x = 1+sin2𝑥‾‾‾‾‾‾‾‾‾‾√
Hence the maximum value of sinx + cosx iS
1+1‾‾‾‾‾√=2‾√
Question 6.
a) lim𝑥→2[x] =
(i) 2 (ii) 3 (iii) 0 (iv) does not exist
b) Evaluate : lim𝑥→2𝑥3−4𝑥2+4𝑥𝑥2−4
Answer:
a) iv) does not exist.
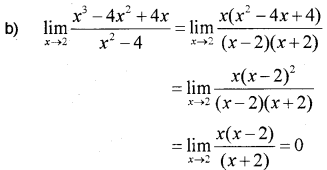
Question 7.
One card is drawn at random from a pack of 52 playing cards. Find the probability that,
a) the card drawn is black.
b) the card is a face card.
c) the card is a black face card.
Answer:

Answer any eight questions from 8 to 17. Each carries 4 scores each. (8 × 4 = 32)
Question 8.
a) If A = {a, b, c}, then write power set of P(A).
b) If the number of subsets with two elements of a set P is 10, then find the total number of elements in set P.
c) Find the number of elements in the power set of P.
Answer:
a) P(A) = {Φ, {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c}}
b) nC2 = 10 ⇒ 𝑛(𝑛−1)2 = 10
⇒ n2 – n – 20 = 0
⇒ (n – 5 )(n + 4) = 0 ⇒ n = 5, -4
Total number of elements in set P is 5
c) Number of elements in power set of P is 25 = 32
Question 9.
Consider the Venn diagram of the Universal set U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13}
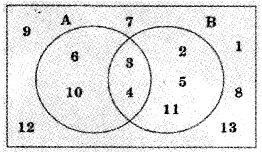
a) Write sets A,B in Roster form.
b) Verify (A∪B)’ = A’∩B’
c) Find n(A∩B)’
Answer:
a) A = {3, 4, 6, 10}; B = {2, 3, 4, 5, 11}
b) From the Venn diagram we can find all the sets.
(A∪B)’ = {1, 7, 8, 9, 12, 13}
A’ = {1, 2, 5, 7, 8, 9, 11, 12, 13}
B’ = {1, 6, 7, 8, 9, 10, 12, 13}
A’∩B’ = {1, 7, 8, 9, 12, 13}
Hence (A∪B)’ = A’∩B’
c) (A∩B)’ = {1, 2, 5, 6, 7, 8, 9, 10, 11, 12, 13}
n((A∩B)’) = 11
Question 10.
Consider the following graphs:
i)
ii)
iii)
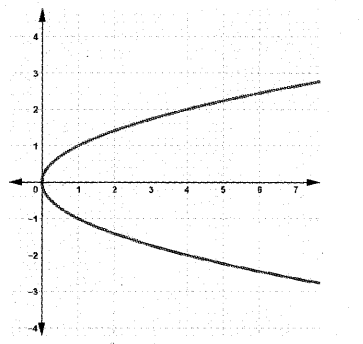
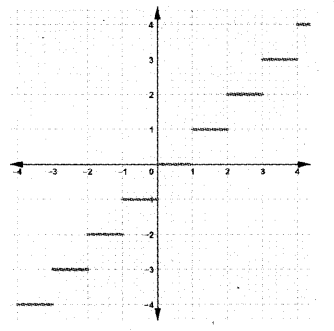
a) Which graph does not represent a function?
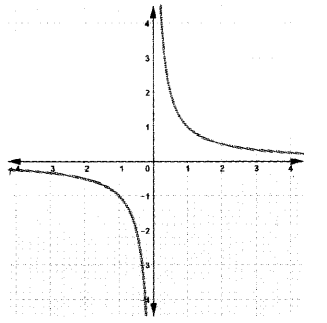
b) Identify the function f(x) = 1𝑥 from the above graph.
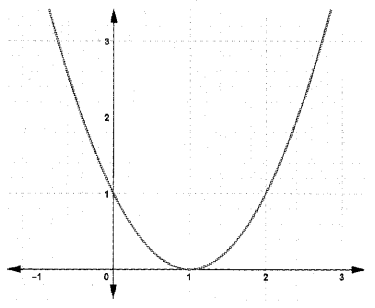
c) Draw the graph of the function f(x) = (x – 1)2
Answer:
a) There are two answers (ii) and (iii)
(vertical line interest at more than two points)
b) i)
c) The graph of f(x) = (x – 1)2 is obtained by shifting the graph of f(x) = x2 to right 1 units.
Question 11.
The figure shows the graph of a function f(x) which is a semi circle centered at origin.
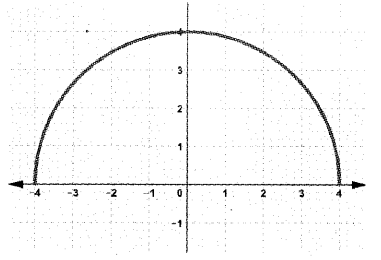
a) Write the domain and range of f(x).
b) Define the function f(x).
Answer:
a) From the graph it is clear that the domain = [-4, 4]; range = [0, 4]
b) The equation of the circle centered at origin with radius 4 is x2 + y2 =16
⇒ y = ±16−𝑥2‾‾‾‾‾‾‾√
y = 16−𝑥2‾‾‾‾‾‾‾√ represent the upper semicircle and y = –16−𝑥2‾‾‾‾‾‾‾√ represent the lower semicircle. Therefore the function is of the form f(x) = 16−𝑥2‾‾‾‾‾‾‾√
Question 12.
a) If 32n+2 – 8n – 9 is divisible by ‘k’ for all n∈N is true, then which one of the following is a value of ‘k’?
(i)8 (ii) 6 (iii) 3 (iv) 12
b) Prove by using the principal of Mathematical Induction P(n) = 1 + 3 + 32 + …….. + 3n-1 = 3𝑛−12 is true for all n∈N
Answer:
a) i) 8 P(1) = 32+2 – 8 – 9 = 64

Question 13.
a) Solve the inequality 2𝑥−13≥3𝑥−24−2−𝑥5
b) Represent the solution on a number line.
Answer:

Question 14.
a) Find the nth term of the sequence 3, 5, 7, ………
b) Find the sum to n terms of the series 3 × 12 + 5 × 22 + 7 × 32 + ……….
Answer:
an = 3 + (n – 1)2 = 2n + 1
The series is the combination of two series 3, 5, 7,…….. and 1, 2, 3,……
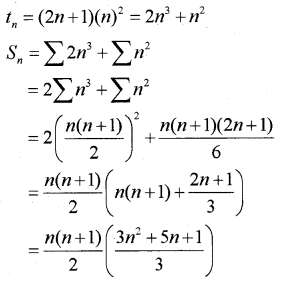
Question 15.
Find the equation of the circle passing through the points (4, 1) and (6, 5) and whose centre is on the line 4x + y = 16
Answer:
Let the equation of the circle be (x – h)2 + (y – k)2 = r2
Since the circle pass through the points (4, 1) and (6, 5)
(4 – h)2 + (1 – h)2 = r2 ……….(1)
(6 – h)2 + (5 – k)2 = r2 ……(2)
4x + y = 16 ……..(3)
Solving the three equations we get h = 3 and k = 4.
(4 – 3)2 + (1 – 4)2 = r2 ⇒ r2 = 10
Hence the equation of the required circle is (x – 3)2 + (y – 4)2 = 10
Question 16.
Consider a point A (4, 8, 10) in space
a) Find the distance of the point A from XY-Plane.
b) Find the distance of the point A from X-axis.
c) Find the ratio in which the line segment joining the point A and B (6, 10, -8) is divided by YZ-plane.
Answer:
a) 10 (z coordinate of the point)
b) The distance from x-axis
= (8)2+(10)2‾‾‾‾‾‾‾‾‾‾‾√=164‾‾‾‾√=241‾‾‾√
c) When the line segment divides the YZ plane its x coordinate will be zero. Let the intersecting point divides the line segment in the ratio k : 1.
![]()
Therefore the ratio 2 : 3.
Question 17.
a) Which one of the following sentences is a Statement?
i) 275 is perfect square.
ii) Mathematics is a difficult subject.
iii) Answer this question.
iv) Today is a rainy day.
b) Verify by method of contradiction: ‘2‾√ is irrational’
Answer:
a) i) 275 is perfect square.
b) Assume that 2‾√ is rational. Then 2‾√ can be written in the form 2‾√ = 𝑝𝑞, where p and q are integers without common factors.
Squaring; 2 = 𝑝2𝑞2 ⇒ 2q2 = p2
⇒ 2 divides p2 ⇒ 2 divides p
Therefore, p = 2k for some integer k.
⇒ p2 = 4k2 ⇒ 2q2 = 4k2 ⇒ q2 = 2k2
⇒ 2 divides q2 ⇒ 2 divides q
Hence p and q have common factor 2, which contradicts our assumption. Therefore, 2‾√ is irrational.
Answer any 5 questions from 18 to 24. Each carries 6 scores. (5 × 6 = 30)
Question 18.
Consider the quadratic equation x2 + x + 1 = 0
a) Solve the quadratic equation.
b) Write the polar form of one of the roots.
c) If the two roots of the given quadratic are α and β. Show that α2 = β
Answer:
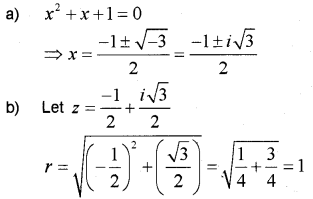
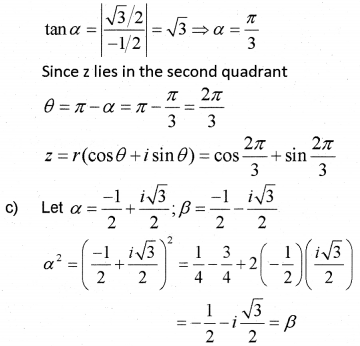
Question 19.
The graphical solution of a system of linear inequalities is shown in the figure.
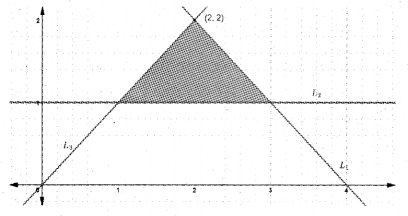
a) Find the equation of the lines L1, L2, L3
b) Find the inequalities representing the solution region.
Answer:
a) L1 line passes through (2, 2) and (4, 0)
Slope = 2−42−0 = -1
Equation is (y – 0) = -1(x – 4) ⇒ x + y = 4
L2 is parallel to the x-axis and passess through (0, 1). Hence the equation is y =1
L3 passes through (0, 0) and (2, 2). Hence the equation is y = x
b) The inequalities that form the shaded region are x + y ≤ 4; y ≥ 1; y ≤ x
Question 20.
a) Which of the following has its middle term independent of x?
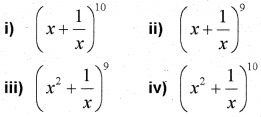
b) Write the expansion of (𝑥2+3𝑥)4
c) Determine whether the expansion of (𝑥2+2𝑥)18 will contain a term containing x10.
Answer:
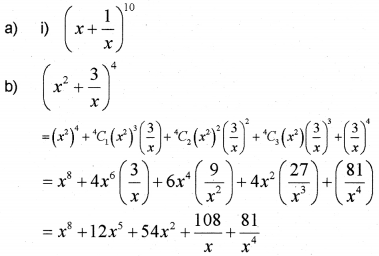

Question 21.
The figure shows an ellipse 𝑥225+𝑦29 = 1 and a line L.
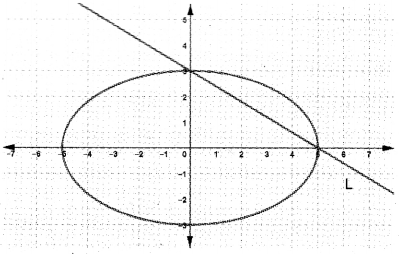
Find the eccentricity and focus of the ellipse.
Find the equation of the line L.
Find the equation of the line parallel to the line L and passing through any one of the foci.
Answer:


Question 22.
a) Find the derivative of y = sin x from the first principal.
b) Find 𝑑𝑦𝑑𝑥, if y = 𝑥5−cos𝑥sin𝑥
Answer:
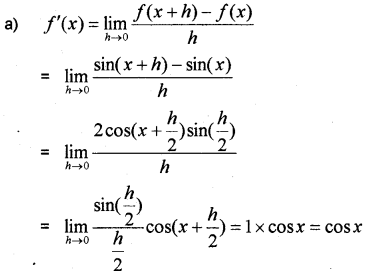
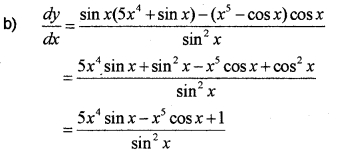
Question 23.
a) Find n, if 12 × (n-1)P3 = 5 × (n+1)P3
b) If nPr=840, nCr=35 , find r.
c) English alphabet has 5 vowels and 21 consonants. How many 4 letter words with two different vowels and two different consonants can be formed without repetition of letters?
Answer:
a) Given; 12(n – 1)P3 = 5(n + 1)P3
⇒ 12(n -1 )(n – 2)(n – 3) = 5 (n + 1)(n)(n – 1)
⇒ 12(n – 2)(n – 3) = 5(n + 1)(n)
⇒ 12(n2 – 5n + 6) = 5n2 + 5n
⇒ 12n2 – 60n + 72 = 5n2 +5n
⇒ 7n2 – 65n + 72 = 0
⇒ 7n2 – 56n – 9n + 72 = 0
⇒ 7n(n – 8) -9 (n – 8) = 0
⇒ (7n – 9)(n – 8) = 0 ⇒ n = 97; 8
Therefore the acceptable value of n = 8
b) nPr = r! × nCr ⇒ 840 = r! × 35 ⇒ r! = 24 ⇒ r = 4
c) Two different vowels can be selected in 5C2.
Two different consonants can be selected in 21C2.
Therefore total numbers of words
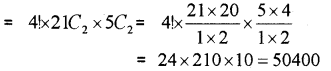
Question 24.
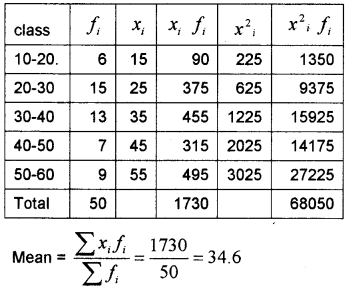
Consider the following distribution:

a) Calculate the mean of the distribution.
b) Find the standard deviation of the distribution.
c) Find the coefficient of variation of the distribution.
Answer:





![Photo of পুরাতন কবিরাজি বই PDF Download 💖[7MB]️](https://bdbookstore.com/wp-content/uploads/2022/01/পরতন-কবরজ-বই-PDF-Download-7MB.png)
![Photo of দরজার ওপাশে pdf download হুমায়ুন আহমেদ | Dorjar opashe pdf Download 💖[7MB]️](https://bdbookstore.com/wp-content/uploads/2022/01/দরজর-ওপশ-pdf-download-হময়ন-আহমদ--Dorjar-opashe-pdf-Download-7MB.png)